binary tree
对于一种数据结构而言,遍历是常见操作。二叉树是一种基本的数据结构,是一种每个节点的儿子数目都不多于2的树。二叉树的节点声明如下:
public class ENode {
private int data;
private ENode left;
private ENode right;
public ENode(int data) {
this.data = data;
}
public ENode getLeft() {
return left;
}
public void setLeft(ENode left) {
this.left = left;
}
public ENode getRight() {
return right;
}
public void setRight(ENode right) {
this.right = right;
}
@Override
public String toString() {
return "ENode{" +
"data=" + data +
", left=" + left +
", right=" + right +
'}';
}
}
二叉树的遍历主要有先序遍历,中序遍历,后序遍历,层序遍历四种方式,我们将介绍每种方式的递归算法和非递归算法:
1、先序遍历
在先序遍历中,访问节点的顺序是根节点-左儿子-右儿子。由于树可以通过递归来定义,所以树的常见操作用递归实现常常是方便清晰的。递归实现的代码如下:
public void pre(ENode eNode){
if(eNode==null){
return;
}
System.out.print(eNode.toString()+"---");
pre(eNode.getLeft());
pre(eNode.getRight());
}
该递归是尾递归,采用栈存储调用信息,我们可以使用栈堆来实现非递归的算法。该算法会沿着当前节点不断获取其左子节点,并将当前节点压到栈中,直到没有左子节点,再从栈中弹出最近的一个节点,获取其右子节点,重复上述操作,直到所有节点都访问完成并且栈为空时结束。具体实现代码如下:
public void pre2(ENode eNode){
if(eNode==null){
return;
}
Stack<ENode> stack=new Stack<ENode>();
while(eNode!=null || !stack.isEmpty()){
while(eNode!=null){
System.out.print(eNode.toString()+"---");
stack.push(eNode);
eNode=eNode.getLeft();
}
if(!stack.isEmpty()){
eNode=stack.pop();
eNode=eNode.getRight();
}
}
}
2、中序遍历
中序遍历是访问完所有左儿子后再访问根节点,最后访问右儿子,即为左儿子-根节点-右儿子。递归实现的代码如下:
public void mid(ENode eNode){
if (eNode==null){
return;
}
mid(eNode.getLeft());
System.out.print(eNode.toString()+"---");
mid(eNode.getRight());
}
中序遍历的一种非递归算法依然是借助栈堆进行,通过沿着当前节点不断获取左子节点并压入栈中,直到当前节点没有左子节点,然后从栈中弹出最近一个节点并打印,然后获取其右子节点,然后重复上述操作,直到所有节点都访问完成并且栈为空时结束。具体实现代码如下:
public void mid1(ENode eNode){
if(eNode==null){
return;
}
Stack<ENode> stack=new Stack<ENode>();
while(eNode!=null || !stack.isEmpty()){
while(eNode!=null){
stack.push(eNode);
eNode=eNode.getLeft();
}
if(!stack.isEmpty()){
eNode=stack.pop();
System.out.print(eNode.toString()+"---");
eNode=eNode.getRight();
}
}
}
有一种不需要借助栈堆就能实现的算法,这种算法包括右线索化和回溯两个点,用右线索化和回溯算法主要是通过分析中序算法我们可以知道,它会沿着当前节点不断获取其左子节点,以最后一个左子节点为开始,再到该左子节点的根节点,再到根节点的右子节点,再到根节点的父节点,利用这个特征我们通过指定该右子节点的右节点为根节点的父节点,形成遍历的线索,我们称之为右线索化。
该算法大致的实现思想如下:若当前树的根节点p有左孩子且未被线索化:将其左孩子的最右结点(可为左孩子本身)指向p,即右线索化,然后p = p->lChild;若p有左孩子但已被线索化,说明该p是回溯上来的,即左孩子已经被访问了,则释放线索化的指针;若p无左孩子,打印p,向上回溯(即p = p->rChild)。
具体实现代码如下:
public void mid2(ENode eNode){
if(eNode==null){
return;
}
while(eNode!=null){
ENode l=eNode.getLeft();
if(l!=null){
while(l.getRight()!=null && l.getRight()!=eNode){
l=l.getRight();
}
if(l.getRight()==null){
l.setRight(eNode);
eNode=eNode.getLeft();
continue;
}else {
l.setRight(null);
}
}
System.out.print(eNode.toString()+"---");
eNode=eNode.getRight();
}
}
3、后序遍历
后序遍历访问节点的顺序是先访问左儿子和右儿子,最后访问节点,即左儿子-右儿子-根节点。递归算法的代码如下:
public void after(ENode eNode){
if(eNode==null){
return;
}
pre(eNode.getLeft());
pre(eNode.getRight());
System.out.print(eNode.toString()+"---");
}
通过栈堆的非递归算法由两种,第一种如下,对于一个节点而言,要实现访问顺序为左儿子-右儿子-根节点,可以利用后进先出的栈,在节点不为空的前提下,依次将根节点,右儿子,左儿子压栈。故我们需要按照根节点-右儿子-左儿子的顺序遍历树,而我们已经知道先序遍历的顺序是根节点-左儿子-右儿子,故只需将先序遍历的左右调换并把访问方式打印改为压入另一个栈即可。最后一起打印栈中的元素。代码如下:
public void after1(ENode eNode){
if(eNode==null){
return;
}
Stack<ENode> stack=new Stack<ENode>();
Stack<ENode> stack1=new Stack<ENode>();
while(eNode!=null || !stack.isEmpty()){
while(eNode!=null){
stack1.push(eNode);
stack.push(eNode);
eNode=eNode.getRight();
}
if(!stack.isEmpty()){
eNode=stack.pop();
eNode=eNode.getLeft();
}
}
while (!stack1.isEmpty()){
eNode=stack1.pop();
System.out.print(eNode.toString()+"---");
}
}
第二种的非递归算法如下: 要访问一个节点的条件上一个访问的节点是右儿子。我们可以增加一个变量Prev来判断当前节点Curr的上一个节点与它的关系来执行相应的操作。若Prev为空(Curr节点是根节点)或者Prev是Curr的父节点,如果Curr存在左孩子则将左孩子压入栈中,如果不存在左孩子存在右孩子则将右孩子压入栈中;若Prev是Curr的左儿子,则Curr的右儿子存在则将其压入栈;否则访问Curr;实现代码如下:
public void after2(ENode eNode){
if(eNode==null){
return;
}
Stack<ENode> stack=new Stack<ENode>();
ENode pre=null;
ENode cur=null;
stack.push(eNode);
while(!stack.isEmpty()){
cur=stack.peek();
if(pre==null || pre.getLeft()==cur || pre.getRight()==cur){
if(cur.getLeft()!=null){
stack.push(cur.getLeft());
}else if(cur.getRight()!=null){
stack.push(cur.getRight());
}
}else if(cur.getLeft()==pre){
if(cur.getRight()!=null){
stack.push(cur.getRight());
}
}else{
System.out.print(cur.toString()+"---");
stack.pop();
}
pre=cur;
}
}
4、层序遍历
层序遍历方式的结果是将二叉树从上到下,从左至右一层一层的遍历。遍历从根节点开始,首先将根节点入队,然后执行循环:节点出队,访问(访问)根节点,将左儿子入队,将右儿子入队,直到队列为空停止。,代码实现如下:
public void fencen(ENode eNode){
Queue<ENode> queue=new LinkedList<ENode>();
queue.offer(eNode);
while(!queue.isEmpty()){
eNode=queue.poll();
System.out.print(eNode.toString()+"---");
if(eNode.getLeft()!=null){
queue.offer(eNode.getLeft());
}
if(eNode.getRight()!=null){
queue.offer(eNode.getRight());
}
}
}
下面我们将对上面的算法进行测试:
public static void create(int[] vals, List<ENode> nodeList){
ENode root=null;
for(int i=0;i<vals.length;i++){
root=new ENode(vals[i]);
nodeList.add(root);
}
for(int j=0;j<vals.length/2-1;j++){
nodeList.get(j).setLeft(nodeList.get(j*2+1));
nodeList.get(j).setRight(nodeList.get(j*2+2));
}
int index=vals.length/2-1;
nodeList.get(index).setLeft(nodeList.get(index*2+1));
if(vals.length%2==1){
nodeList.get(index).setRight(nodeList.get(index*2+2));
}
}
public static void main(String[] args) {
int[] value={2,4,8,3,6,4,8,2,6,9,4};
List<ENode> nodeList=new LinkedList<ENode>();
create(value,nodeList);
root=nodeList.get(0);
new ErChaShu1().pre(root);
System.out.println();
new ErChaShu1().pre2(root);
System.out.println();
new ErChaShu1().mid(root);
System.out.println();
new ErChaShu1().mid1(root);
System.out.println();
new ErChaShu1().mid2(root);
System.out.println();
new ErChaShu1().after(root);
System.out.println();
new ErChaShu1().after1(root);
System.out.println();
new ErChaShu1().after2(root);
System.out.println();
new ErChaShu1().fencen(root);
}
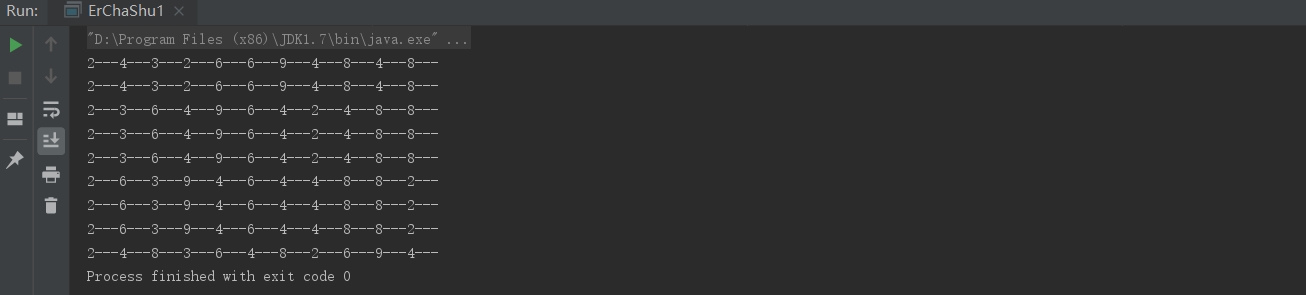
运行结果: