knapsack problem
在M件物品取出若干件放在空间为W的背包里,每件物品的体积为W1,W·2……Wn,与之相对应的价值为P1,P2……Pn。求出获得最大价值的方案。
本文将使用动态规划法、贪心算法、回溯法实现0-1背包问题的求解。
通用对象的创建
物品对象:
public class Knapsack {
//物品重量
private int weight;
//物品价值
private int value;
/***
* 构造器
*/
public Knapsack(int weight, int value) {
this.value = value;
this.weight = weight;
}
public int getWeight() {
return weight;
}
public int getValue() {
return value;
}
public String toString() {
return "[weight: " + weight + " " + "value: " + value + "]";
}
}
动态规划法
针对0-1背包问题,使用动态规划算法的重点在于掌握使用动态规划法求解问题的分析方法和实现思想。
分析方法:问题实例 P(n)的最优解S(n)蕴含问题实例 P(n-1)的最优解S(n-1);在S(n-1)的基础上构造S(n) 。
实现思想:自底向上的迭代求解和基于记忆功能的自顶向下递归。
结合动态规划算法的分析方法和实现思想,下面是其对背包问题的应用分析:
我们可以将问题分解为将前n件物品放入容量为j的背包中”这个子问题,若只考虑第n件物品的策略(放或不放),那么就可以转化为一个只牵扯前n-1件物品的问题。如果不放第n件物品,那么问题就转化为“前n-1件物品放入容量为j的背包中”;如果放第n件物品,那么问题就转化为“前n-1件物品放入剩下的容量为j-c[n]的背包中”,此时能获得的最大价值就是v[n-1][j-c[n]]再加上通过放入第i件物品获得的价值w[n]。
v[n,j]表示前n件物品恰放入一个容量为j的背包可以获得的最大价值,结合动态规划法的实现思想,我们可以将解决问题的实现分为求解最优解和求解最优背包组成两部分:
求解最优值:
- 若 j < wn, 则 : v[n,j] = v[n-1,j];
- 若 j >= wn, 则:v[n,j] = max{v[n-1,j], vn + v[n-1,j-wn]}。
求解最优背包组成: - 若 v[n,j] > v[n-1,j] 则 背包 n 被选择放入 b[n],
- 接着求解前 n-1 个背包放入 j-wn 的总承重中, 于是应当判断 v[n-1, j-wn]和 v[n-2,j-wn]的大小, 决定 背包 n-1 是否被选择。
- 依次逆推,直至总承重为零。
关键代码:
public class KnapsackProblem {
/** 指定背包 */
private Knapsack[] bags;
/** 总承重 */
private int totalWeight;
/** 给定背包数量 */
private int n;
/** 前 n 个背包,总承重为 totalWeight 的最优值矩阵 */
private int[][] bestValues;
/** 前 n 个背包,总承重为 totalWeight 的最优值 */
private int bestValue;
/** 前 n 个背包,总承重为 totalWeight 的最优解的物品组成 */
private ArrayList<Knapsack> bestSolution;
public KnapsackProblem(Knapsack[] bags, int totalWeight) {
this.bags = bags;
this.totalWeight = totalWeight;
this.n = bags.length;
if (bestValues == null) {
bestValues = new int[n+1][totalWeight+1];
}
}
/**
* 求解前 n 个背包、给定总承重为 totalWeight 下的背包问题
*
*/
public void solve() {
System.out.println("给定背包:");
for(Knapsack b: bags) {
System.out.println(b);
}
System.out.println("给定总承重: " + totalWeight);
// 求解最优值
for (int j = 0; j <= totalWeight; j++) {
for (int i = 0; i <= n; i++) {
if (i == 0 || j == 0) {
bestValues[i][j] = 0;
}
else
{
// 如果第 i 个背包重量大于总承重,则最优解存在于前 i-1 个背包中,
// 注意:第 i 个背包是 bags[i-1]
if (j < bags[i-1].getWeight()) {
bestValues[i][j] = bestValues[i-1][j];
}
else
{
// 如果第 i 个背包不大于总承重,则最优解要么是包含第 i 个背包的最优解,
// 要么是不包含第 i 个背包的最优解, 取两者最大值,这里采用了分类讨论法
// 第 i 个背包的重量 iweight 和价值 ivalue
int iweight = bags[i-1].getWeight();
int ivalue = bags[i-1].getValue();
bestValues[i][j] =
Math.max(bestValues[i-1][j], ivalue + bestValues[i-1][j-iweight]);
} // else
} //else
} //for
} //for
// 求解背包组成
if (bestSolution == null) {
bestSolution = new ArrayList<Knapsack>();
}
int tempWeight = totalWeight;
for (int i=n; i >= 1; i--) {
if (bestValues[i][tempWeight] > bestValues[i-1][tempWeight]) {
bestSolution.add(bags[i-1]); // bags[i-1] 表示第 i 个背包
tempWeight -= bags[i-1].getWeight();
}
if (tempWeight == 0) { break; }
}
bestValue = bestValues[n][totalWeight];
}
/**
* 获得前 n 个背包, 总承重为 totalWeight 的背包问题的最优解值
* 调用条件: 必须先调用 solve 方法
*
*/
public int getBestValue() {
return bestValue;
}
/**
* 获得前 n 个背包, 总承重为 totalWeight 的背包问题的最优解值矩阵
* 调用条件: 必须先调用 solve 方法
*
*/
public int[][] getBestValues() {
return bestValues;
}
/**
* 获得前 n 个背包, 总承重为 totalWeight 的背包问题的最优解值矩阵
* 调用条件: 必须先调用 solve 方法
*
*/
public ArrayList<Knapsack> getBestSolution() {
return bestSolution;
}
}
数据测试代码:
public class KnapTest {
public static void main(String[] args) {
Scanner in=new Scanner(System.in);
System.out.println("请输入物品个数:");
int n=in.nextInt();
System.out.println("请输入背包容量:");
int totalWeight=in.nextInt();
Knapsack[] bags = new Knapsack[n];
System.out.println("请依次输入物品的重量(w)和价值(v)——以w,v的形式输入:");
for(int i=0;i<n;i++){
String str=in.next();
String[] strs=str.split(",");
bags[i]=new Knapsack(Integer.parseInt(strs[0]),Integer.parseInt(strs[1]));
}
KnapsackProblem kp = new KnapsackProblem(bags, totalWeight);
kp.solve();
System.out.println(" -------- 该背包问题实例的解: --------- ");
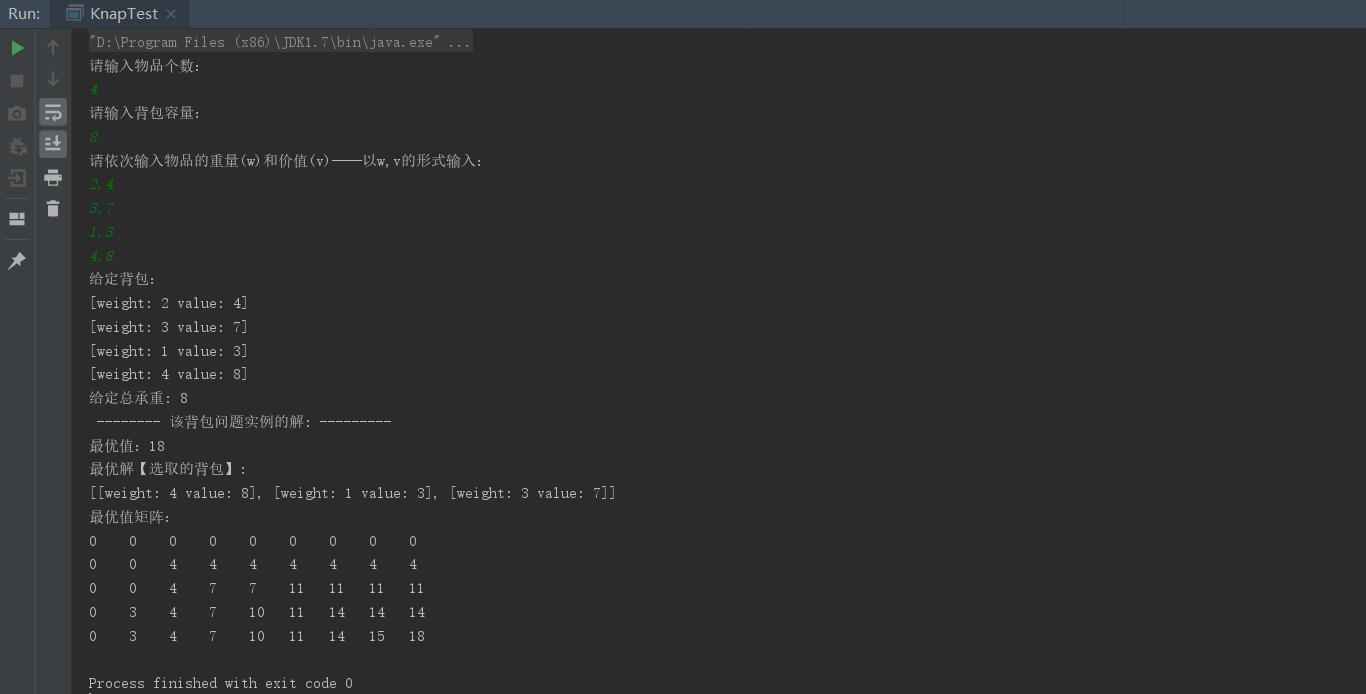
System.out.println("最优值:" + kp.getBestValue());
System.out.println("最优解【选取的背包】: ");
System.out.println(kp.getBestSolution());
System.out.println("最优值矩阵:");
int[][] bestValues = kp.getBestValues();
for (int i=0; i < bestValues.length; i++) {
for (int j=0; j < bestValues[i].length; j++) {
System.out.printf("%-5d", bestValues[i][j]);
}
System.out.println();
}
}
}
测试结果:
贪心算法
贪心算法是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的仅是在某种意义上的局部最优解。所以针对背包问题,其实现思想是依次选择单位重量价值最高的物品,直到总重量超过了背包的能装的物品总重量。具体实现步骤如下:
1、通过计算每个物品单位重量的价值,然后按对物品按单位重量价值从高到低进行排序;
2、对排序后的集合进行遍历,以背包剩余空间小于等于0为结束条件,依次从集合中取出物品装入背包中,并计算装入背包的物品的总价值。
核心代码:
public class KnapsackProblem1 {
/** 指定背包 */
private Knapsack[] bags;
/** 总承重 */
private int totalWeight;
/** 给定背包数量 */
private int n;
/** 总承重为 totalWeight 的最优值 */
private int bestValue;
/** 前 n 个背包,总承重为 totalWeight 的最优解的物品组成 */
private ArrayList<Knapsack> bestSolution;
public KnapsackProblem1(Knapsack[] bags, int totalWeight) {
this.bags = bags;
this.totalWeight = totalWeight;
this.n = bags.length;
}
public void solve(){
System.out.println("给定背包:");
for(Knapsack b: bags) {
System.out.println(b);
}
System.out.println("给定总承重: " + totalWeight);
//计算每个物品的单位重量价值并排序
for(int i=0;i<n-1;i++){
for(int j=n-1;j>i;j--){
if(bags[j].getValue()*1.00/bags[j].getWeight()>bags[j-1].getValue()*1.00/bags[j-1].getWeight()){
Knapsack kk=new Knapsack();
kk=bags[j-1];
bags[j-1]=bags[j];
bags[j]=kk;
}
}
}
//遍历排练后的数组求最优解
int i=0;
// 求解背包组成
if (bestSolution == null) {
bestSolution = new ArrayList<Knapsack>();
}
while(totalWeight>0){
bestSolution.add(bags[i]);
totalWeight-=bags[i].getWeight();
bestValue+=bags[i].getValue();
i++;
}
//如果放进最后一个物品后超重了,那么需要拿出最后一个物品
if(totalWeight<0){
bestSolution.remove(--i);
bestValue-=bags[i].getValue();
}
}
/**
* 获得前 n 个背包, 总承重为 totalWeight 的背包问题的最优解值
* 调用条件: 必须先调用 solve 方法
*
*/
public int getBestValue() {
return bestValue;
}
/**
* 获得前 n 个背包, 总承重为 totalWeight 的背包问题的最优解值矩阵
* 调用条件: 必须先调用 solve 方法
*
*/
public ArrayList<Knapsack> getBestSolution() {
return bestSolution;
}
}
数据测试代码:
public class KnapTest1 {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
System.out.println("请输入物品个数:");
int n = in.nextInt();
System.out.println("请输入背包容量:");
int totalWeight = in.nextInt();
Knapsack[] bags = new Knapsack[n];
System.out.println("请依次输入物品的重量(w)和价值(v)——以w,v的形式输入:");
for (int i = 0; i < n; i++) {
String str = in.next();
String[] strs = str.split(",");
bags[i] = new Knapsack(Integer.parseInt(strs[0]), Integer.parseInt(strs[1]));
}
KnapsackProblem1 kp = new KnapsackProblem1(bags, totalWeight);
kp.solve();
System.out.println(" -------- 该背包问题实例的解: --------- ");
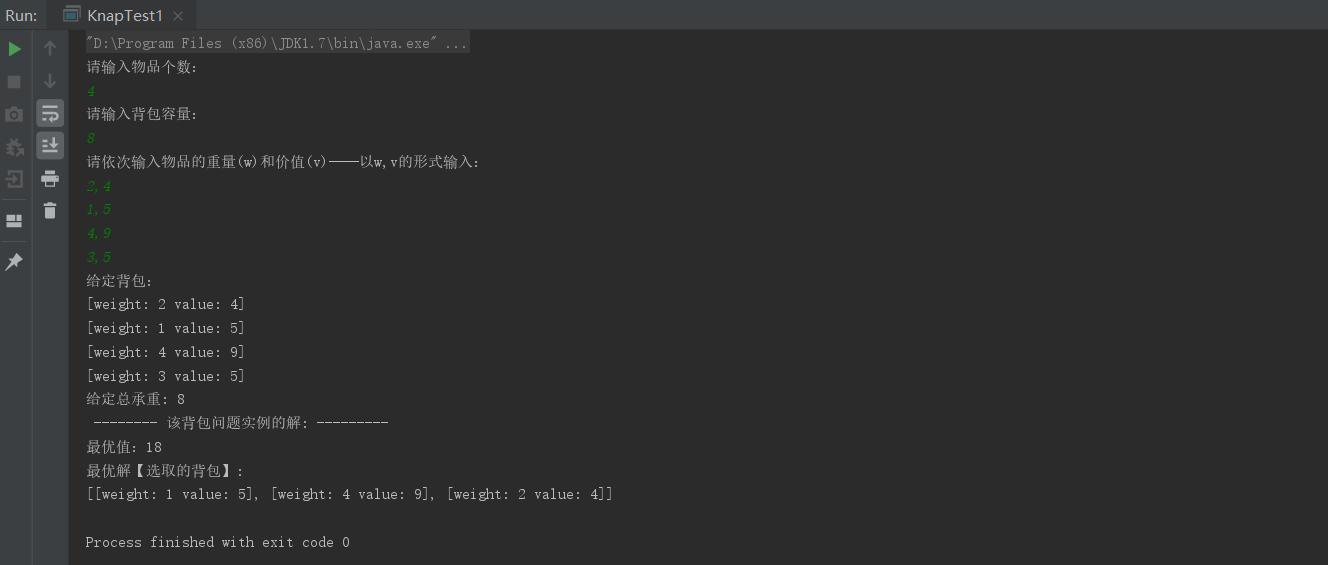
System.out.println("最优值:" + kp.getBestValue());
System.out.println("最优解【选取的背包】: ");
System.out.println(kp.getBestSolution());
}
}
测试结果:
回溯法
回溯算法的基本思想是在包含问题的所有解的解空间树中,按照深度优先搜索的策略,从根结点出发深度探索解空间树。当探索到某一结点时,要先判断该结点是否包含问题的解,如果包含,就从该结点出发继续探索下去,如果该结点不包含问题的解,则逐层向其祖先结点回溯。所以回溯算法对于背包问题的应用可以分为两个部分:搜索最优解和剪枝:
在回溯开始之前,首先对于背包中的物品按照单位重量价值进行排序,方便于后面右子树的剪枝操作
搜索最优解:对于背包中的每一个物品,可以选择放入(左子树)或者不放入(右子树)。依次对每个节点进行搜索,得到最优解。
剪枝:对于左子树,如果放入物品的重量已经超过了背包的容量,则直接进行剪枝。对于右子树,是否可以直接跳过本层的物品,直接下一层的搜索操作,这要取决于当前背包剩余的容量,依次取背包中剩余的物品中单位重量价值最大的物品(跳过本层物品),最终能否超过此前找到的最优解,如果能够超过,则可以向右搜索,不能超过,则右节点变为死节点。 对于寻找剩余物品的最高价值上界,按照背包中剩余空间依次取剩下的物品,当空间不足以取下一个 物品时,则将下一个物品的单位重量价值折算到现在的剩余空间中去计算理想最高上界。
核心代码:
public class KnapsackProblem2 {
/** 指定背包 */
private Knapsack[] bags;
/** 总承重 */
private int totalWeight;
/** 给定背包数量 */
private int n;
/** 总承重为 totalWeight 的最优值 */
private int bestValue;
/** 前 n 个背包,总承重为 totalWeight 的最优解的物品组成 */
private ArrayList<Knapsack> bestSolution;
private int tempValue;
private int tempWeight;
public KnapsackProblem2(Knapsack[] bags, int totalWeight) {
this.bags = bags;
this.totalWeight = totalWeight;
this.n = bags.length;
}
public void solve(int t){
//已经搜索到根节点
if(t>n-1){
if(tempValue > bestValue){
bestValue = tempValue;
}
return;
}
//搜索左边节点
if(tempWeight + bags[t].getWeight()<= totalWeight){
tempWeight += bags[t].getWeight();
tempValue += bags[t].getValue();
solve(t+1);
tempWeight -= bags[t].getWeight();
tempValue -= bags[t].getValue();
}
//不装入这个物品,直接搜索右边的节点
if( Bound(t+1) >= bestValue){
solve(t+1);
}
}
//用于计算剩余物品的最高价值上界
public int Bound(int k) {
int maxLeft = tempValue;
int leftWeight = totalWeight - tempWeight;
//尽力依照单位重量价值次序装剩余的物品
while (k <= n - 1 && leftWeight > bags[k].getWeight()) {
leftWeight -= bags[k].getWeight();
maxLeft += bags[k].getValue();
k++;
}
//不能装时,用下一个物品的单位重量价值折算到剩余空间。
if (k <= n - 1) {
maxLeft += bags[k].getValue()/ bags[k].getWeight() * leftWeight;
}
return maxLeft;
}
/**
* 获得前 n 个背包, 总承重为 totalWeight 的背包问题的最优解值
* 调用条件: 必须先调用 solve 方法
*
*/
public int getBestValue() {
return bestValue;
}
}
数据测试代码:
public class KnapTest2 {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
System.out.println("请输入物品个数:");
int n = in.nextInt();
System.out.println("请输入背包容量:");
int totalWeight = in.nextInt();
Knapsack[] bags = new Knapsack[n];
System.out.println("请依次输入物品的重量(w)和价值(v)——以w,v的形式输入:");
for (int i = 0; i < n; i++) {
String str = in.next();
String[] strs = str.split(",");
bags[i] = new Knapsack(Integer.parseInt(strs[0]), Integer.parseInt(strs[1]));
}
KnapsackProblem2 kp = new KnapsackProblem2(bags, totalWeight);
kp.solve(0);
System.out.println(" -------- 该背包问题实例的解: --------- ");
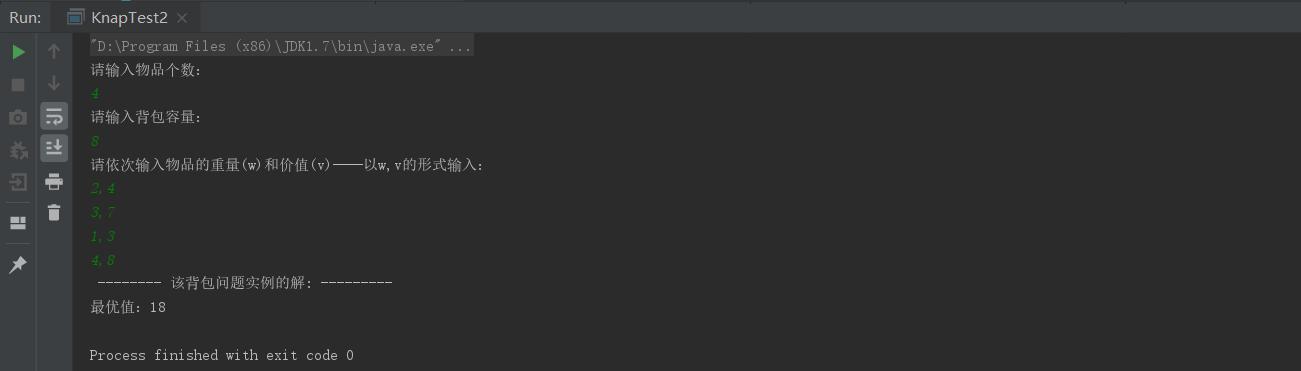
System.out.println("最优值:" + kp.getBestValue());
}
}
public class KnapTest2 {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
System.out.println("请输入物品个数:");
int n = in.nextInt();
System.out.println("请输入背包容量:");
int totalWeight = in.nextInt();
Knapsack[] bags = new Knapsack[n];
System.out.println("请依次输入物品的重量(w)和价值(v)——以w,v的形式输入:");
for (int i = 0; i < n; i++) {
String str = in.next();
String[] strs = str.split(",");
bags[i] = new Knapsack(Integer.parseInt(strs[0]), Integer.parseInt(strs[1]));
}
KnapsackProblem2 kp = new KnapsackProblem2(bags, totalWeight);
kp.solve(0);
System.out.println(" -------- 该背包问题实例的解: --------- ");
System.out.println("最优值:" + kp.getBestValue());
}
}
测试结果:
求解效率的比较和分析
| 算法 | 时间复杂度 | 优点 | 缺点 | 改善点 | | —– | —– | —– |—– |—–| | 动态规划 | O(nm) | 最优解 | 速度慢 | 递归方程求解 | | 贪心算法 | O(nlogn) |速度快 | 不一定是最优解 |启发式方法 | |回溯法 | O(n*2n) | 最优解 | 速度慢 | 剪枝 |
