data structure and algorithm
我希望每个人对算法和数据结构是什么有一个深刻的认识,所以我们会在每一篇的文章的开始给你灌输下面的这些知识点:
1、数据结构是一门研究组织数据方式的学科,有了编程语言也就有了数据结构,学好数据结构可以让你写出更漂亮更高效的代码(时间复杂度和空间复杂度);
2、算法其实就是解决我们生活中遇到的问题的计算方法;
3、程序=数据结构+算法;要学好数据结构和算法就要在日常生活中把遇到的问题尝试用程序去解决
4、数据结构是实现一个算法的基础,所以想要学好算法,需要把数据结构学到位;
5、数据结构分为线性结构和非线性结构;线性结构的特点是数据元素之间存在一对一的线性关系;
6、线性结构又有顺序存储结构和链式存储结构两种的存储结构,顺序存储结构中存储元素是连续的,而链式存储结构中存储元素不一定是连续的;
递归算法
递归就是方法自己调用自己,每次调用时传入不同的变量,递归有助于编程者解决复制的问题,同时可以让代码变得简洁;
递归算法的执行过程分 递推和回归两个阶段。在 递推阶段,把较复杂的问题(规模为n)的求解推到比原问题简单一些的问题(规模小于n)的求解。在回归阶段,当获得最简单情况的解后,逐级返回,依次得到稍复杂问题的解
递归调用机制图解:
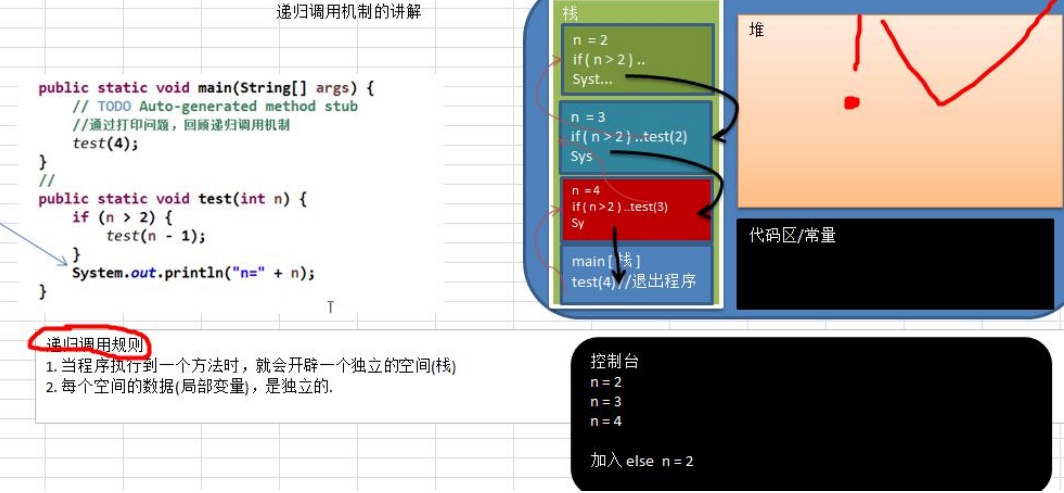
从递归的调用机制我们可以总结出以下递归需要遵守的重要原则:
1、执行一个方法时,就创建一个新的受保护的独立空间(栈空间);
2、方法的局部变量是独立的,不会相互影响,比如n变量;
3、如果方法中使用的是引用类型变量(比如数组),就会共享该引用类型的数据;
4、递归必须向退出递归的条件逼近,否则就会无限递归,出现StackOverflowError;
5、当一个方法执行完毕,或者遇到return,就会返回,遵守谁调用就将结果返回给谁,同时当方法执行完毕或者返回时,该方法也就执行完毕;
迷宫问题
迷宫问题其实通过不同的策略控制着棋子向四个不同的方向走,通过不断递归调用这个方法去试错,走得通就递归走下一步,走不通就回溯到上一步尝试其他的走法,最终就可能走出一条正确的道路;
实现代码:
public class MiGong {
public static void main(String[] args) {
int[][] map = new int[8][7];
for (int i = 0; i < 7; i++) {
map[0][i] = 1;
map[7][i] = 1;
}
for (int i = 0; i < 8; i++) {
map[i][0] = 1;
map[i][6] = 1;
}
map[3][1] = 1;
map[3][2] = 1;
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 7; j++) {
System.out.print(map[i][j] + " ");
}
System.out.println();
}
setWay(map, 1, 1);
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 7; j++) {
System.out.print(map[i][j] + " ");
}
System.out.println();
}
}
//使用递归回溯来给小球找路
//说明
//1. map 表示地图
//2. i,j 表示从地图的哪个位置开始出发 (1,1)
//3. 如果小球能到 map[6][5] 位置,则说明通路找到.
//4. 约定: 当map[i][j] 为 0 表示该点没有走过 当为 1 表示墙 ; 2 表示通路可以走 ; 3 表示该点已经走过,但是走不通
//5. 在走迷宫时,需要确定一个策略(方法) 下->右->上->左 , 如果该点走不通,再回溯
public static boolean setWay(int[][] map, int i, int j) {
if(map[6][5] == 2) { // 通路已经找到ok
return true;
} else {
if(map[i][j] == 0) { //如果当前这个点还没有走过
//按照策略 下->右->上->左 走
map[i][j] = 2; // 假定该点是可以走通.
if(setWay(map, i+1, j)) {//向下走
return true;
} else if (setWay(map, i, j+1)) { //向右走
return true;
} else if (setWay(map, i-1, j)) { //向上
return true;
} else if (setWay(map, i, j-1)){ // 向左走
return true;
} else {
//说明该点是走不通,是死路
map[i][j] = 3;
return false;
}
} else { // 如果map[i][j] != 0 , 可能是 1, 2, 3
return false;
}
}
}
}
八皇后问题
八皇后问题是一个以国际象棋为背景的问题:如何能够在8×8的国际象棋棋盘上放置八个皇后,使得任何一个皇后都无法直接吃掉其他的皇后?为了达到此目的,任两个皇后都不能处于同一条横行、纵行或斜线上。
实现思路:
1、确定递归结束条件:当我们完成第八行棋子的摆放之后递归调用结束;
2、从第一行第一列开始放棋,每放一步棋就去检查是否与之前的棋子冲突,如果不冲突就继续到下一行开始放棋;
3、通过判断当前行的棋子与之前各行的棋子是否放在同一列或者放在同一对角线上来判断是否冲突;
4、如果当前行的每一列都发送冲突,回溯到上一行,更换上一行棋子的位置之后再递归调用进行下一行棋子的摆放;
实现代码:
public class Queue8 {
public static void main(String[] args) {
Queue8 queue8=new Queue8();
queue8.check(0);
System.out.println(count);
}
static int count=0;
int max=8;
int[] array=new int[max];
public void print(){
count++;
for(int i=0;i<max;i++){
System.out.printf(array[i]+" ");
}
System.out.println();
}
public boolean isCT(int n){
for(int i=0;i<n;i++){
if(array[i]==array[n] || Math.abs(n-i)==Math.abs(array[n]-array[i])){
return false;
}
}
return true;
}
public void check(int n){
if(n==max){
print();
return;
}
for(int i=0;i<max;i++){
array[n]=i;
if(isCT(n)){
check(n+1);
}
}
}
}
