data structure and algorithm
我希望每个人对算法和数据结构是什么有一个深刻的认识,所以我们会在每一篇的文章的开始给你灌输下面的这些知识点:
1、数据结构是一门研究组织数据方式的学科,有了编程语言也就有了数据结构,学好数据结构可以让你写出更漂亮更高效的代码(时间复杂度和空间复杂度);
2、算法其实就是解决我们生活中遇到的问题的计算方法;
3、程序=数据结构+算法;要学好数据结构和算法就要在日常生活中把遇到的问题尝试用程序去解决
4、数据结构是实现一个算法的基础,所以想要学好算法,需要把数据结构学到位;
5、数据结构分为线性结构和非线性结构;线性结构的特点是数据元素之间存在一对一的线性关系;
6、线性结构又有顺序存储结构和链式存储结构两种的存储结构,顺序存储结构中存储元素是连续的,而链式存储结构中存储元素不一定是连续的;
图
图是一种非线性的数据结构,其中结点可以具有零个或多个相邻元素。两个节点之间的连接称为边,节点也可以称为顶点;
图能够表示多对多的关系,而线性表局限于一个直接前驱和一个直接后继的关系,树也只能有一个直接前驱;
图的表示方式
图的表示方式有两种:二维数组表示(邻接矩阵);链表表示(邻接表);
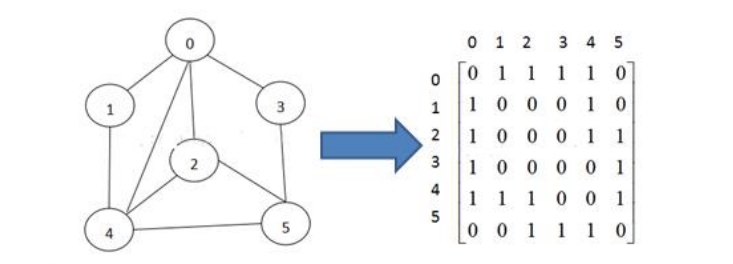
邻接矩阵
邻接矩阵是表示图形中顶点之间相邻关系的矩阵,对于N个顶点的图而言,矩阵是row和colum表示的1到n个点。
邻接表
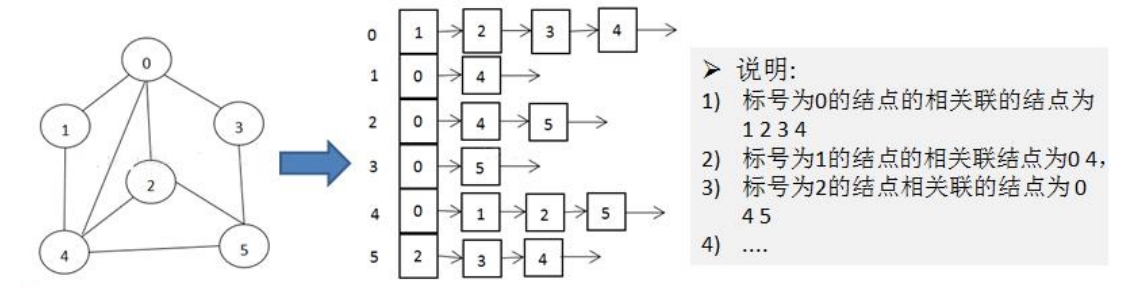
邻接矩阵需要为每一个顶点都分配n个边的空间,其实有很多边是不存在的,会造成空间的一定损失;
邻接表的实现只关心存在的边,不关心不存在的边,因此没有空间浪费,邻接表由数组+链表组成。
图的深度优先遍历(DFS)
基本思想:
1、深度优先遍历,从初始访问结点出发,初始访问结点可能有多个邻接结点,深度优先遍历的策略就是首先访问第一个邻接结点,然后再以这个被访问的邻接结点作为初始结点,访问它的第一个邻接结点,可以这样理解:每次都在访问完当前结点后首先访问当前结点的第一个邻接结点。
2、我们可以看到,这样的访问策略是优先往纵向挖掘深入,而不是对一个结点的所有邻接结点进行横向访问。 3)显然,深度优先搜索是一个递归的过程;
3、显然,深度优先搜索是一个递归的过程;
代码实现:
/*
实现步骤:
1)访问初始结点V,并标记结点V为己访问。
2)查找结点V的第一个邻接结点w。
3)若w存在,则继续执行4,如果w不存在,则回到第1步,将从V的下一个结点继续。
4)若w未被访问,对w进行深度优先遍历递归(即把w当做另一个V,然后进行步骤123)。
5)查找结点V的w邻接结点的下一个邻接结点,转到步骤3。
*/
public static void dfs(int val){
stack.push(val);
while(!stack.isEmpty()){
int value= (int) stack.pop();
System.out.print(value+"-->");
isvisited[value]=true;
int ff=getLast(value);
while (ff!=-1){
if(!isvisited[ff]){
stack.push(ff);
}
ff=getNext(value,ff);
}
}
}
public static int getLast(int val){
for(int i=list.size()-1;i>=0;i--){
if(ins[val][i]==1){
return i;
}
}
return -1;
}
public static int getNext(int val,int value){
for(int i=value-1;i>=0;i--){
if(ins[val][i]==1){
return i;
}
}
return -1;
}
图的广度优先遍历(WFS)
基本思想:
)类似于一个分层搜索的过程,广度优先遍历需要使用一个队列以保持访问过的结点的顺序,以便按这个顺序来访问这些结点的邻接结点。
代码实现:
/*
实现步骤:
1)访问初始结点V并标记结点V为己访问。
2)结点V入队列
3)当队列非空时,继续执行,否则算法结束。
4)出队列,取得队头结点U0
5)查找结点U的第一个邻接结点wo
6)若结点U的邻接结点w不存在,则转到步骤3;否则循环执行以下三个步骤:
6.1若结点w尚未被访问,则访问结点w并标记为己访问。
6.2结点w入队列
6.3查找结点U的继w邻接结点后的下一个邻接结点w,转到步骤6。
*/
public static void wfs(int val){
queue.offer(val);
while(!queue.isEmpty()){
int value= (int) queue.poll();
System.out.print(value+"-->");
isvisited[value]=true;
int ff=getFisrt(value);
while(ff!=-1){
if(!isvisited[ff]){
queue.offer(ff);
}
ff=getFNext(value,ff);
}
}
}
public static int getFisrt(int val){
for(int i=0;i<list.size();i++){
if(ins[val][i]==1){
return i;
}
}
return -1;
}
public static int getFNext(int val,int value){
for(int i=value+1;i<list.size();i++){
if(ins[val][i]==1){
return i;
}
}
return -1;
}
